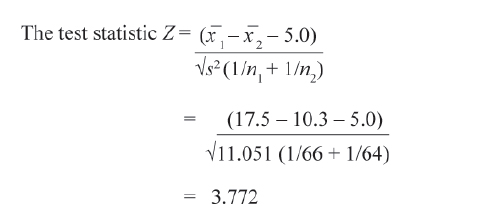In randomized clinical trials the researcher is interested in not just testing difference in treatment outcome of new drug and a standard drug as control but wants to know whether the difference is of clinical relevance. This article outlines the method for framing the null and alternate hypotheses for testing the clinically relevant effects. The method is explained through illustrations.  

Background: Statistical significance testing (SST) has been serving the important purpose of advancement of research in all walks of life. Researchers utilize the statistical significance testing for illustrating the importance of their research findings. Statistical significance has become a rigidly defined and enforced criterion for the publication of research in most of the scientific journals. The journals accept manuscript documenting findings with details on study design, sample size, methods of statistical analysis, and statistical significance of research findings.

Karl Pearson laid the foundation for significance testing as early as 1901. Classical statistical inference involving statistical significance testing is an anonymous hybrid of ideas developed by Ronald Fisher on one hand and Jery Neyman and Egon Pearson on the other.

Fisher, in significant testing approach, promoted inductive inference from particular to general or from sample to population. Fisher’s views of inductive inference focused on the rejection of null hypothesis based on P = (X|H_o), that is, probability of data (X) given the truth of null hypothesis (H₀) is true. This probability (p value), according to Fisher, represented an objective way for researchers to assess the plausibility of the null hypothesis.

The Neyman-Pearson, under hypothesis testing approach, formulated two competing hypothesis, the null hypothesis (H₀) and the alternative hypothesis (H_a). Their framework introduced the probabilities of committing two kinds of errors, false rejection (Type I error) and false acceptance (Type II error) of the null hypothesis. They introduced a concept of power of the test, that is, the probability of rejecting the null hypothesis when it is false.

Fisher’s statistical testing has no reference to alternative hypothesis, concept of Type-II error, and power of test. However, the power in Fisher’s approach is somewhat implicit when he refers to sensitivity of an experiment. (J Clin Prev Cardiol 2014;3(4):147-50)

Null Hypothesis

The starting point in Statistical Significance Testing involves setting of a null hypothesis. In framing the null hypothesis the guidelines are as follows:
 

• Start with outlining the research hypothesis mentioning explicitly the effect of interest for which researchers wish to find evidence.
• Translate this research hypothesis to a statistical alternative hypothesis (H_a).
• Set up null hypothesis (H₀) as the statement that the desired effect of interest is not present.

The most commonly used null hypothesis is

Although the most important goal in SST relates to testing the above hypotheses, the other goals of hypothesis testing are as follows:
 

• Testing of homogeneity for consistency of results at multiple sites
• Testing for statistical assumptions involved in using a particular testTo advance a theoryThe tests of significance mainly involve testing of proportions, means, variances, etc. Further the SST for each of these parameters deal with different situations represented in Fig. 1.

In view of above, to use SST in different situations researchers are required to understand the assumptions and principles involved in using a test along with the relevance of the same in a particular research context.

Directionality: 

As already mentioned in most situations, the SST are applied for testing the difference of proportions or averages. In experimental studies, investigating the efficacy of a new drug in relation to a standard drug, the null hypothesis and alternative hypothesis are presented as under:

Here P is the measure of treatment outcome and subscripts 1 and 2 are for new and standard drugs.

The results based on a two-tailed test will indicate whether the difference is significant or not. The reportingof mere significance of a difference is not informative enough. On the other hand, the inference in terms of the beneficial effect of the treatment is a more informative result. This type of inference is based on a one-tailed test. Thus in testing of hypothesis, consideration of directionality in alternative hypothesis is critical. To eliminate any ambiguity, it is important to state direction as part of a null hypothesis/alternative hypothesis pair. Importantly one-sided tests are less likely to ignore a real effect. A nonsignificant result under two-tailed test can sometimes become a significant result by the use of a one-tailed hypothesis.

It may be mentioned that there are situations where one has to use a two-tailed test. Particularly, in observational studies for comparing the outcomes across subgroups, a two-tailed test will be used. In general, if one does not have a specific direction firmly in mind a two-sided test should be used. As an alternative, one can use all the three alternatives, that is, testing hypothesis once in each direction and thereafter for a two-sided test, thereby drawing the inference based on all.

Clinical Significance :

It may be noted that the differences which are statistically significant are not always of practical importance. Conversely the difference which is not shown as statistically significant may be at times of clinical relevance. In view of this, a question is generally asked whether a statistically significant result is necessarily a noteworthy result. A clinical researcher would like to test whether the difference which is statistically significant is large enough to make an impact on the treatment outcome. In most randomized control trials (RCTs), the researcher will be interested in knowing whether the new drug is superior over the standard drug by a desired magnitude. For this, the researcher doing the study has to explicitly indicate what difference will be of clinical relevance to establish the superiority of new drug over the standard drug. Let this difference of interest be “δ.” Based on this information about δ a null and alternative hypothesis could be appropriately framed for testing its significance.

The null and alternative hypothesis in this situation would be


Illustrations:

Example 1

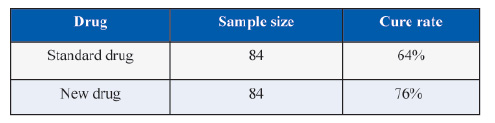
A randomized clinical trial was conducted to test the claim that a new drug is superior over the standard drug in terms of 10% higher efficacy. The results of RCT comparing the drugs produced the following results.



In this case the null and alternative hypotheses are

	The efficacy of new drug is higher to that of standard drug by a magnitude less than or equal to 10%.
	The efficacy of new drug is higher to that of standard drug by a magnitude more than 10%.

Here subscripts 1 and 2 are for standard and new drug, respectively.

In this example, the estimated values of efficacy (cure rate) are
P₂ = 0.76
P₁ = 0.64

Combined P = (P₁ + P₂)/2 = 0.70

Standard Normal Deviate (Z) test is used for this.

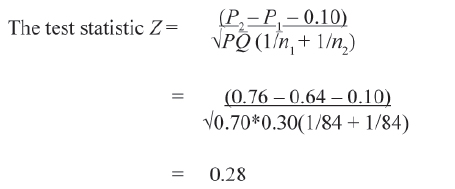
This is one tail test. The p-value corresponding to Z = 0.28 equals 0.39. The result is not statistically significant at 5% level of significance. Hence the claim that new drug is superior in efficacy by more than 10% is not accepted.

The value of Z statistic for testing the absolute difference in the cure rate of two drugs equals 1.68 (p value 0.0465, for one-tailed tests). The difference is statistically significant with p < 0.05.

In this example, the new drug has significantly higher efficacy in comparison to the standard drug. But the superiority is not more than 10% as claimed.

Example 2

In another trial on comparison of new intervention with the standard treatment of care on duration of hospital stay yielded the following results.


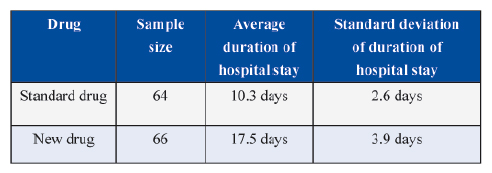
The researcher will consider new intervention more effective only if reduction in duration of hospital stay is 5 or more days.

In this case with usual notations the null and alternative hypotheses are

Here μ denotes the average and subscripts 1 and 2 for intervention and standard treatment of care, respectively.

In this example, estimated values of μ 1 and μ 2 are

1. Pearson K. The scope of biometrika. Biometrika. 1901;1:1–2.
2. Risher RA. Statistical Methods of Research Workers. Edinburgh: Oliver and Boyd; 1925.
3. Risher RA. Statistical methods and scientific induction. J Royal Stat Soc Ser B. 1955;17:69–78.
4. Neyman J, Pearson ES. On the use and interpretation of certain test criteria for purposes of statistical inference. Part I. Biometrika. 1928;20A:175–240.